Portfolio
Algorithmic Trading Environment
Soon …
Python/C++ 2D CR SPECTRA code
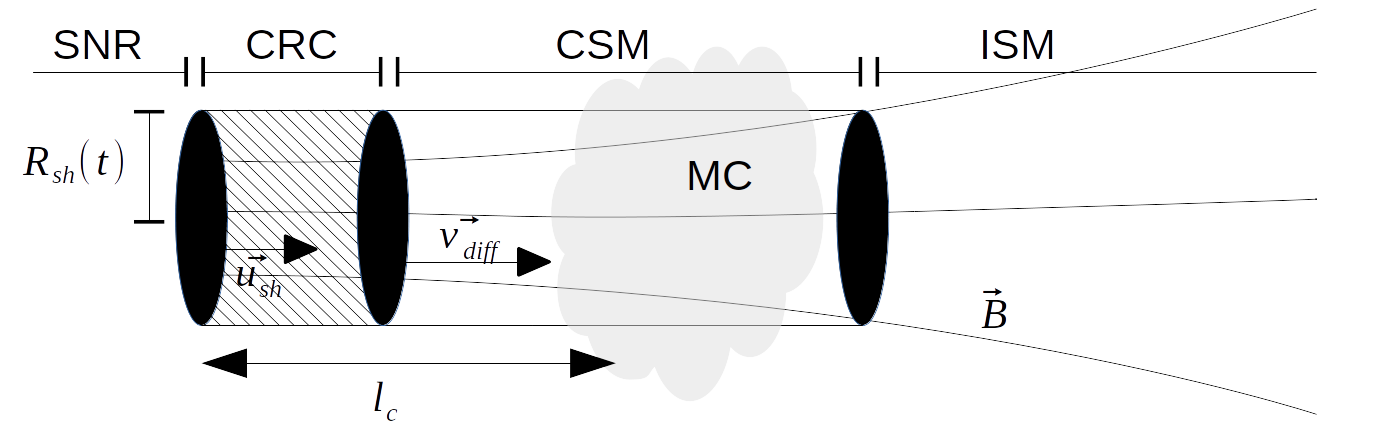
A Cosmic Rays Self Propagation Escaping and Confinment TRAnsport code (CR SPECTRA)
The Cosmic Rays Self Propagation Escaping and Confinement TRAnsport code (CR SPECTRA) describe the non-linear relation between the way high energy particles are released in the Interstellar Medium from Supernova Remnant and the magnetic turbulence they generate in a close environment around the source, turbulence which contributes to confine particles close to the accelerator and then to affect the escape process itself. The code consists in solving the following non-linearly coupled system of four equations $$ \begin{aligned} \frac{\partial P_\mathrm{p}}{\partial t} + V_\mathrm{A} \frac{\partial P_\mathrm{p}}{\partial z} & = \frac{\partial}{\partial z} \left( \kappa_{zz} \frac{\partial P_\mathrm{p}}{\partial z} \right) + \frac{E}{3} \left\{ V_\mathrm{A}, P_\mathrm{p} \right\} - \frac{4}{3} \frac{\partial V_\mathrm{A}}{\partial z} P_\mathrm{p} + Q_{\mathrm{p}, \mathrm{inj}} \\ \frac{\partial P_\mathrm{e}}{\partial t} + V_\mathrm{A} \frac{\partial P_\mathrm{e}}{\partial z} & = \frac{\partial}{\partial z} \left( \kappa_{zz} \frac{\partial P_\mathrm{e}}{\partial z} \right) + \frac{E}{3} \left\{ V_\mathrm{A}, P_\mathrm{e} \right\} - \frac{4}{3} \frac{\partial V_\mathrm{A}}{\partial z} P_\mathrm{e} + Q_{\mathrm{p}, \mathrm{inj}} + Q_{\mathrm{e}, \mathrm{sync}}(P_\mathrm{e}) \\ \frac{\partial I_+}{\partial t} + V_\mathrm{A} \frac{\partial I_+}{\partial z} & = - I_+ \frac{\partial V_\mathrm{A}}{\partial z} + \Gamma_\mathrm{g}^+ I_+ - \Gamma_\mathrm{d}^+ (I_+ - I_+^0) \\ \frac{\partial I_-}{\partial t} + V_\mathrm{A} \frac{\partial I_-}{\partial z} & = - I_- \frac{\partial V_\mathrm{A}}{\partial z} + \Gamma_\mathrm{g}^- I_- - \Gamma_\mathrm{d}^+ (I_- - I_-^0) \end{aligned} $$ in a two dimensional phase space where the first dimension represents the spatial direction in which galactic scale magnetic field lines are correlated (see the figure above) and the second dimension represents the energy associated to the resonant Alfvén waves interacting with the released CRs. The system is solved using first and second order finite difference methods for explicit solvers and implicit methods for the diffusion term. This system has some particularities: - The diffusion coefficient $$\kappa_{zz}$$ depends on the turbulence rates $$I_\pm$$ - An energy log scale has been used to solve energy related terms - The Interstellar Medium model is inhomogeneous leading to a space variable initial diffusion coefficient $$\kappa_{zz}(z, t = 0)$$ - Cosmic Rays (protons p and electrons e) are injected through a term $$Q_{\mathrm{p,e,inj}}$$ itself depending on the turbulence rates $$I_\pm$$ - Cosmic Rays generate turbulence $$I_\pm$$ through linear thermal instability terms $$\Gamma_g^\pm$$ - CRs generated turbulence $$I_\pm$$ is progressively damped ($$\Gamma_\mathrm{d}^\pm$$) down to the background turbulence state $$I_\pm^0$$ according the Interstellar Medium plasma physical properties
Sub-grid CRs diffusion coefficients in the RAMSES code
Soon …
Rectangular Hilbert Grid Generator
A tool I developed by grabbing pieces of code on the web and reading papers about Hilbert algorithms. The objective of this tool is to be able to create a grid to line transformation of a randomly sized \(2^L \times 2^h\) 2D grid which can be used to attribute cells in a contiguous way to \(2^N\) calculation processes in the case of a 2D grid cell numerical simulation for example.
Small Scale Turbulence code
Development of a Python analytical code allowing to modelise the magnetic turbulence generated by Cosmic Ray instabilities and damped by interaction with a partially ionized plasma. The following equation is solved:
\[\Gamma_\mathrm{g} + \Gamma_\mathrm{in} = 0\]where \(\Gamma_\mathrm{g}\) corresponds to the magnetic turbulence growth rate and depends mainly on the Cosmic Rays distribution, energy and pressure gradient, and \(\Gamma_\mathrm{in}\) corresponds to the magnetic turbulence damping rate which mainly depends on the physical properties of the plasma we consider the waves are propagating in: density, temperature, ionization rate, turbulence rate. Each of both terms is subject to a deep bibliographical theoretical and experimental study. The models of wave growth and damping are then implemented in the code and allow to solve the above equation.
Because Cosmic Rays are charged particles (here we consider protons), they are sensible to magnetic turbulence and their propagation properties are also affected by magnetic turbulence. Depending on the interstellar medium phase I have chosen, I have been able to calculate the mean free path of Cosmic Rays as a function of their kinetic energy for my small scale turbulence model (continuous colored lines) and compare it with the standard model which doesn’t take in account medium properties (black dashed line).
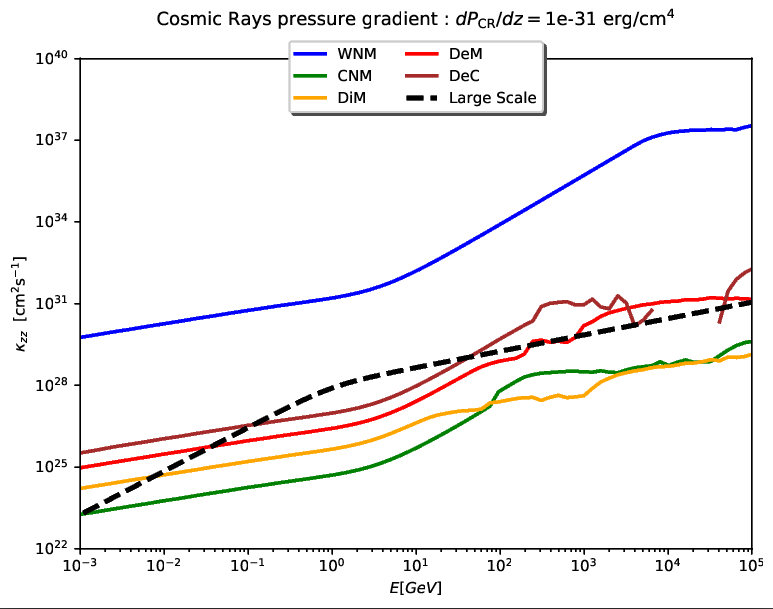
More details here.
3D N-Body numerical simulation
Development of a 3-Dimensional gravitational N-body simulation in C++ for the fun! The code has the following features:
- Brute force calculation (CPU based)
- Object Oriented structure
- Second order time symmetric Verlet solver
Here below is an example of the trajectories of 10 particles selected from a batch of 1000 particles. Colors represent the norm of the velocity of each particle.
Popularization website in Physics
Popularization website about Physics. The aim of this project is to help people to have a better understanding of what is Physics: models, methods and processes. The website is well referenced by Google and get more than 2000 unique users per month and content is recommended by University professors for their students.
